Gate 2020 (XE-C) Full Solution and Explanation | Unit - I | Gate Material Science 2020 Question & Answers

GATE material science question papers with solution and explanation free pdf download , Download GATE 2020 question papers on material science, GATE Previous Year Solved Papers [PDF] – XE, GATE engineering science question papers with solutions, GATE 2020 Material science, material science solutions, GATE  XE paper 2020.

Here you can find the 2020 GATE Material Science (XE-C) paper with answer key and full explanation in pdf given below:

This set of Engineering Materials Science "Problems & Answers" are based on “GATE 2020 (XE-C)”

GATE 2020 (XE-C)

QUESTIONS, ANSWERS & EXPLANATION

UNIT - I (QUESTION 1 to 9)

Unit – I contains 9 numbers of questions (From Question 1 to Question 9) including MCQ and numerical problem each of which carry one mark.

1) A Pb-Sn sample of eutectic composition, containing α- and β- phases, is examined in a scanning electron microscope. The α-phase contains ~97 wt.% Pb (atomic number 82) while β-phase contains ~99 wt.% Sn (atomic number 50). The ratio of number of backscattered electrons escaping from α-phase to that from β-phase would be:

A. Less than 1

B. Equal to 1

C. Greater than 1

D. Equal to 0

Correct Answer is "C"

For scanning electron microscope,

The number of backscattered electrons (BSE) ∝ mean atomic number

(BSE)_α/(BSE)_β = (Mean atomic number)_α/(Mean atomic number)_β = 82/50 = 1.64 i.e. greater than 1

2) Smallest or minimum feature size that can be theoretically resolved in an optical Microscope does NOT depend on:

A. Refractive index of the medium between the lens and the focal point

B. Intensity of radiation

C. Wavelength of radiation

D. Numerical aperture of the objective lens

Correct Answer is "B"

Theoretical limit of an optical microscope can be calculated using Abbe’s diffraction limit formula

Abbe’s diffraction limit formula for lateral resolution (i.e. XY),

d_l or d_x,y = 𝜆/2𝑁𝐴 = 𝜆/2(𝑛𝑠𝑖𝑛𝛼)

Abbe’s diffraction limit formula for axial resolution (i.e Z),

d_A or d_z = 2𝜆/(𝑁𝐴)² = 2𝜆/(𝑛𝑠𝑖𝑛𝛼)²

Where,

𝜆 = Wavelength of the radiation

NA = Numerical aperture of the objective lens

n = Refractive index of the medium between the lens and the focal point

α = Half of the angular aperture of the objective lens

3) Following diagram shows a square 2-D lattice with a hexagonal motif (dark colored). The rotational symmetry element that must be present in the system is:

A. Six-fold rotation

B. Two-fold rotation

C. Three-fold rotation

D. Four-fold rotation

Correct Answer is "B"

n-fold rotational symmetry of an object means if the object rotates about an axis by an angle of 360°/n then it will repeat itself.

The given figure is a combination of hexagon and square.

Hexagon has six-fold rotational symmetry.

Square has four-fold rotational symmetry.

So the rotational symmetry of the given figure is the G.C.M of hexagon and square’s rotational symmetry.

Hence the given object has two-fold rotational symmetry

4) Density of states, D(E), in a three dimensional solid varies with energy (E) as

A. 𝐸^1/2

B. 𝐸⁰

C. 𝐸^-1/2

D. 𝐸^3/2

Correct Answer is "A"

We know that,

Density of states for 1D, D(E)_1D ∝ 𝐸^-1/2

Density of states for 2D, D(E)_2D ∝ 𝐸⁰

Density of states for 3D, D(E)_3D ∝ 𝐸^1/2

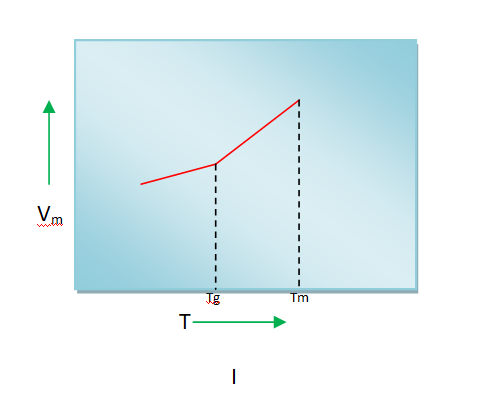
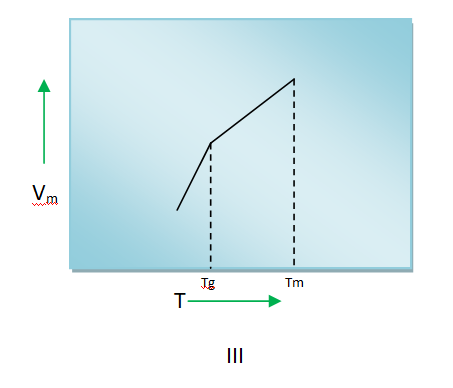
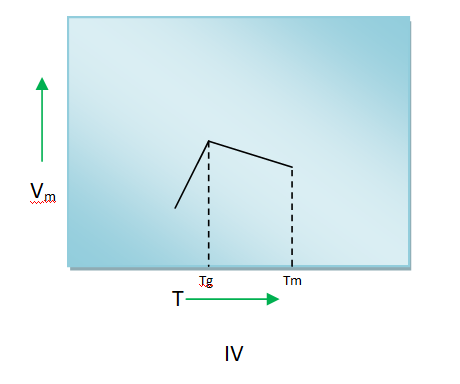
5) The variation of molar volume (V_m) of a liquid showing glass transition temperature (T_g) while cooling from its melting temperature (T_m) is depicted by

A. I

B. II

C. III

D. IV

Correct Answer is "A"

Variation of molar volume with temperature of a liquid upon cooling are shown below

Curve A is for totally amorphous material (having glass transition temperature)

Curve B is for semi-crystalline material (having glass transition temperature)

Curve C is for crystalline material (no glass transition temperature)

Curve A or Curve B matches only with the figure I of the given problem

6) Find the correct match between polymer name in column I and the monomer type in column II.

COLUMN-I	COLUMN-II
I. Polyethylene	(P)
II. Polypropylene	(Q)
III. Polyvinyl chloride	(R)
IV. Polystyrene	(S)

A. I-P, II-S, III-R, IV-Q

B. I-R, II-Q, III-S, IV-P

C. I-S, II-P, III-Q, IV-R

D. I-S, II-R, III-Q, IV-P

Correct Answer is "C"

Monomer of the given polymers are shown below

COLUMN-I	COLUMN-II
I. Polyethylene	S.
II. Polypropylene	P.
III. Polyvinylchloride	Q.
IV. Polystyrene	R.

7) A ceramic has a fracture toughness (K_IC) of 1 MPa.m^1/2. If this ceramic is to be exposed to a maximum stress (σ) of 200MPa, the maximum value of half crack length ‘a’ (in micrometer, μm), below which the material does not fail, is ______ μm (round off to one decimal place). Loading condition for the sample is shown in the schematic. Assume geometrical factor f=1.2.

Correct Answer is "5.3 – 5.7"

We know that,

K_IC = Yσ √(𝝅𝒂)

where,

K_IC = Fracture toughness = 1 MPa.m^1/2

Y = Geometrical factor = f = 1.2

σ = Maximum stress = 200 MPa

𝒂 = half of the internal crack length = ?

so,

1 = 1.2 × 200 × √(𝝅𝒂)

⇒𝒂 = (𝟏/(𝟏.𝟐 × 𝟐𝟎𝟎))² × (𝟏/𝝅)

⇒𝒂 = 5.526 × 10-6 m =5.526 nm = 5.5 nm (rounded off to one decimal place)

8) A ceramic material is periodically heated and cooled between 25°C and a higher temperature, T_f. During thermal cycling, the material remains dimensionally constrained. The material can withstand a maximum compressive stress of 200 MPa without failure. Material's coefficient of thermal expansion is 7.5 x 10^-6 °C^-1 and modulus of elasticity (E) is 200 GPa. The lowest value of T_f (in °C) at which material will fail is _______°C (round-off to the nearest integer). Assume that there is no plastic deformation during thermal cycling.

Correct Answer is "157 - 159"

We know that,

σ = Eα Δ𝑻 = Eα (T_f – T_i)

where,

σ = Maximum compressive stress = 200 MPa = 200 × 10⁶ Pa

E = Modulus of elasticity = 200 GPa = 200 × 10⁹ Pa

α = Material’s coefficient of thermal expansion = 7.5 × 10^-6 °C^-1

T_i = Initial or lowest temperature = 25°C

T_f = Final or highest temperature = ?

So, 200 × 10⁶ = 200 × 10⁹ × 7.5 × 10^-6 × (T_f – 25)

⇒T_f = 158.3°C

9) During homogeneous solidification of a liquid metal, the radius of critical nucleus (in nanometer, nm) at a temperature T_s which is below the melting point (T_m), is ______ nm (round-off to one decimal place). Given that 𝛾_sl (solid liquid interfacial energy) is 0.18 J.m^-2 and Δ𝐺_v (change in volume free energy upon transformation from liquid to solid) at Ts is 0.18 x10⁹ J.m^-3.

Correct Answer is "1.9 – 2.1"

We know that,

r^* = - (𝟐𝛾_sl)/(Δ𝐺_v)

where,

r^* = critical radius for stable solid particle during homogeneous nucleation = ?

𝛾_sl = solid liquid interfacial energy = 0.18 J.m^-2

Δ𝐺_v = change in volume free energy = 0.18 × 109 J.m^-3

So, r^* = - (𝟐 × 𝟎.𝟏𝟖)/(𝟎.𝟏𝟖 × 𝟏𝟎⁹) = - 2 × 10^-9 (negative sign means critical radius decreases as temperature decreases)

⇒│ r^*│ = 2 × 10^-9 m = 2 nm

Click on the following link given below to download the 2020 XE-C paper Unit-I with complete solutions and explanations.

Download Click here

READ NOW: Gate 2020 (XE-C) Full Solution and Explanation Unit - II

READ NOW: Try online topic wise Practice Test

Let me know if this post is helpful or not?
I am trying my best to gather more and more objective type questions on this site for your best practice. If you have any queries about any questions given above then don't hesitate to comment below or you can also directly contact me through  materialscienceonline4u@gmail.com.

MaterialScienceOnline is made to provide you all types of chapter-wise objective (Multiple Choice, Multiple Select and Numerical) questions, answers, and explanations as well as a chapter-wise various practice tests or quiz to catalyst your competitive exam preparation. Various top-rated Material Science and Engineering pdf books are also available here.

Thank you for visiting this site. If you think this post is helpful then share this post as well as this website with your friends.