Phase Diagram All Formulas For Numerical Problems | Material Science Formula For Numerical Problems

In this place, you will get all types of numerical problem-solving formulas on the topic of "PHASE DIAGRAM" on one page. This formula will help you to solve different types of problems on "PHASE DIAGRAM" very easily. Check out all this formula given below before solving Numerical Problems on "PHASE DIAGRAM" given on this site or anywhere.

PHASE DIAGRAM

FORMULA

Formula 1

Used to Calculate: Mass fraction of liquid phase, binary isomorphous system

W_L = {(C_α - C₀) / (C_α - C_L)}

Where,
W_L = Mass fraction of liquid phase, binary isomorphous system
C_α = Composition of α phase
C₀ = Overall alloy composition (in terms of one of the components)
C_L = Composition of L (liquid) phase

Formula 2

Used to Calculate: Mass fraction of α solid-solution phase, binary isomorphous system

W_α = {(C₀ - C_L) / (C_α - C_L)}

Where,
W_α = Mass fraction of α solid-solution phase, binary isomorphous system
C₀ = Overall alloy composition (in terms of one of the components)
C_α = Composition of α phase
C_L = Composition of L (liquid) phase

Formula 3

Used to Calculate: Volume fraction of α phase

V_α = {v_α / (v_α + v_β)}

Where,
V_α = Volume fraction of α phase
v_α = Volum of α phase
v_β = Volum of β phase

Formula 4

Used to Calculate: Volume Fraction of α phase from the mass fraction

V_α = [(W_α/ρ_α) / { (W_α/ρ_α) + (W_β/ρ_β)}]

Where,
V_α = Volume fraction of α phase
W_α = Mass fraction of α solid-solution phase
ρ_α = Density of the α phase
W_β = Mass fraction of β solid-solution phase
ρ_β = Density of β phase

Formula 5

Used to Calculate: Mass fraction of α phase from volume fraction

W_α = [(V_αρ_α) / {(V_αρ_α) + (V_βρ_β)}]

Where,
W_α = Mass fraction of α solid-solution phase
V_α = Volume fraction of α phase
ρ_α = Density of the α phase
V_β = Volume fraction of β phase
ρ_β = Density of β phase

Formula 6

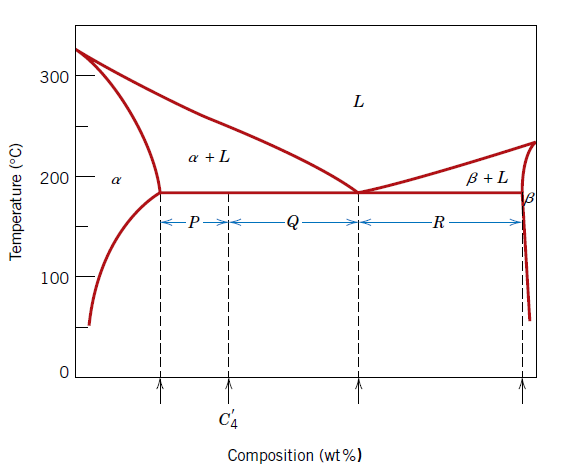
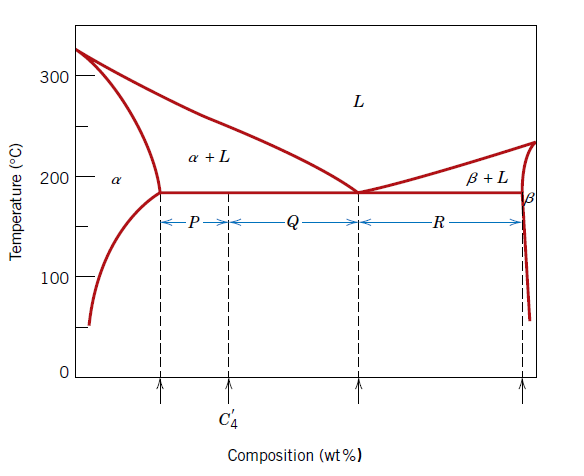
Used to Calculate: Mass fraction of eutectic micro constituent for binary eutectic system

Image may be subjected to copyright

W_e = P/(P + Q)

Where,
W_e = Mass fraction of eutectic micro constituent for binary eutectic system
P, Q = Lengths of tie-line segments as shown in figure

Formula 7

Used to Calculate: Mass fraction of primary α micro constituent for binary eutectic system

Image may be subjected to copyright

W_α' = Q/(P + Q)

Where,
W_α' = Mass fraction of primary α micro constituent for binary eutectic system
P, Q = Lengths of tie-line segments as shown in figure

Formula 8

Used to Calculate: Mass fraction of total α phase for a binary eutectic system

Image may be subjected to copyright

W_α = (Q + R)/(P + Q + R)

Where,
W_α = Mass fraction of total α phase for a binary eutectic system
P, Q, R = Lengths of tie-line segments as shown in figure

Formula 9

Used to Calculate: Mass fraction of β phase for a binary eutectic system

Image may be subjected to copyright

W_β = P/(P + Q + R)

Where,
W_β = Mass fraction of β phase for a binary eutectic system
P, Q, R = Lengths of tie-line segments as shown in figure

Formula 10

Used to Calculate: Number of Phase or Component present in a system, Number of degrees of freedom (Gibbs phase rule)

P + F = C + N

Where,
P = Number of phase present in a given system
F = Number of Degrees of freedom or Number of externally controlled variables (e.g., temperature, pressure, composition) that must be specified to define the state of the system completely.
C = Number of components in the system
N = Number of noncompositional variables (e.g., pressure and temperature)

Formula 11

Used to Calculate: Total Number of Variables in a system

V = P(C - 1) + N

Where,
V = Total number of variables in a system
P = Number of phase present in a given system
C = Number of components in the system
N = Number of noncompositional variables (e.g., pressure and temperature)
P(C - 1) = Total number of composition variables

Formula 12

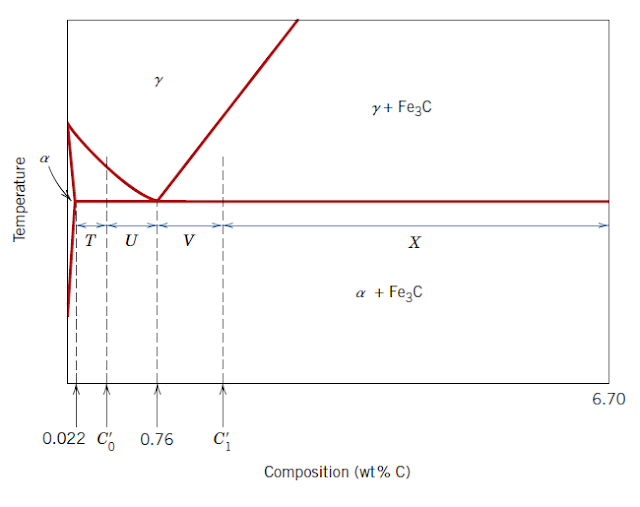
Used to Calculate: Mass fraction of pearlite for a hypoeutectoid Fe - C alloy

Image may be subjected to copyright

W_P = T/(T + U) = {(C₀^' - 0.022) / 0.74}

Where,
W_P = Mass fraction of pearlite
C₀^' = Composition of a hypoeutectoid alloy in weight percent carbon
T, U = Lengths of tie-line segments as shown in figure

Formula 13

Used to Calculate: Mass fraction of pro eutectoid α ferrite phase for a hypoeutectoid Fe - C alloy

Image may be subjected to copyright

W_α' = U/(T + U) = {(0.76 - C₀^') / 0.74}

Where,
W_α' = Mass fraction of proeutectoid α ferrite phase
C₀^' = Composition of a hypoeutectoid alloy in weight percent carbon
T, U = Lengths of tie-line segments as shown in figure

Formula 14

Used to Calculate: Mass fraction of pearlite for a hypereutectoid Fe - C alloy

Image may be subjected to copyright

W_P = X/(V + X) = {(6.70 - C₁^') / 5.94}

Where,
W_P = Mass fraction of pearlite
C₁^' = Composition of a hypereutectoid alloy in weight percent carbon
X, V = Lengths of tie-line segments as shown in figure

Formula 15

Used to Calculate: Mass fraction of pro eutectoid Fe₃C phase for a hypoeutectoid Fe - C alloy

Image may be subjected to copyright

W_(Fe3C) = V/(V + X) = {(C₁^' - 0.76) / 5.94}

Where,
W_(Fe3C) = Mass fraction of proeutectoid Fe₃C phase
C₁^' = Composition of a hypereutectoid alloy in weight percent carbon
X, V = Lengths of tie-line segments as shown in figure

REFERENCES:

Materials Science and Engineering: an Introduction (9E) by William D. Callister, Jr., and David G. Rethwisch.

Click here to know details about this book and download it in pdf format.

Materials Science and Engineering: A First Course by Raghavan.

Click here to know details about this book and download it in pdf format.

Suggestions to Readers:

Hey Readers, Do you read carefully all the formulas based on "PHASE DIAGRAM" given above? so why are you waiting for? Let's see how these formulas are used in Numerical problems.

Click here to visit the Numerical Problems on "PHASE DIAGRAM".

Or you can also test your skill by practice some problems based on "PHASE DIAGRAM".

Click here to practice Numerical problems on "PHASE DIAGRAM".

MaterialScienceOnline is made to provide you all types of chapter-wise objective (Multiple Choice, Multiple Select and Numerical) questions, answers, and explanations as well as a chapter-wise various practice tests or quiz to catalyst your competitive exam preparation. Various top-rated Material Science and Engineering pdf books are also available here.

Thank you for visiting this site. If you think this post is helpful then share this post as well as this website with your friends.